An
r-unform
n-vertex hypergraph
H is said to have the Manickam–Miklós–Singhi (MMS) property if for every assignment of weights to its vertices with nonnegative sum, the number of edges whose total weight is nonnegative is at least the minimum degree of
H. In this talk I will show that for
n>
10r3, every
r-uniform
n-vertex hypergraph with equal codegrees has the MMS property, and the bound on
n is essentially tight up to a constant factor. An immediate corollary of this result is the vector space Manickam–Miklós–Singhi conjecture which states that for
n ≥ 4k and any weighting on the
1-dimensional subspaces of
Fqn with nonnegative sum, the number of nonnegative
k-dimensional subspaces is at least
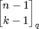
. I will also discuss two additional
generalizations, which can be regarded as analogues of the Erdős–Ko–Rado theorem on
k-intersecting families.
Joint work with Benny Sudakov.
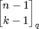 . I will also discuss two additional
generalizations, which can be regarded as analogues of the Erdős–Ko–Rado theorem on k-intersecting families.
. I will also discuss two additional
generalizations, which can be regarded as analogues of the Erdős–Ko–Rado theorem on k-intersecting families.